FDTD(Finite-Difference Time-Domain)
基础概念
电场
每个原子里面都有绕原子核心运动的电子(经典力学上是这么说),原子核中有质子。电子带负电,质子带正电。当正负相中和,物体对外表现中性。否则表现为带电。
宏观上,带电体之间会相互作用,同极相斥,异极相吸。这种相互作用力叫做电场力。
带电体不管静止和运动,都会产生电场。静止的称为静电场,运动的称为感应电场。
电场会使其中的电荷受力,可使其运动。因此电场具有势能,就像重力会产生重力势能一样。电场中两点间电势的差值叫做电势差(电压)

电场强度为E = F/q。单位为牛顿每库伦,符号为N/C。其中q是试探电荷量,F是电荷在电中受到的力。另一单位是伏特每米,符号为V/m。E=U/d,其中U是电压,d是电场中两点的距离。他们是等效的:
从电场力的公式出发,F = Eq,将E的单位N/C代入,得到F的单位是N。
> 从电势差的公式出发,U = Ed,将E的单位V/m代入,得到U的单位是V。由于电势差U和距离d的单位分别是伏特和米,而1伏特等于1焦耳每库仑(J/C),因此1V/m = 1J/(C·m) = 1(N·m)/(C·m) = 1N/C。
1 焦耳 是1牛的力作用于1米的距离
电荷量的单位是库仑(coulomb)C。1C的电荷量相当于6.25×1018个电子所带的电荷量,一个普通大小的物体很难保持多于千分之一库仑的净电荷。

- 电场会随距离而减弱 E=kQ / r^2
- 空间的电场强度是矢量,方向是电场力作用的方向。
- 线性运动的电荷不会产生变化的电场
- 空间任一点的电场强度是该点多个电荷所产生的电场强度的矢量和。
- 电场虽然看不见,摸不着,但是一种物质, 具有能量和动量。就像扔的一块石头一样。唯一不同的是,这种物质没有静止的质量
这种电子的定向运动就产生了电流。物体内部分子的排列杂乱无章,使这些“分子电流”在物体内部互相抵消,总体没有环形电流,但一旦物体被磁化,分子就被有序排列,总体就产生了环形电流,也就有了磁性。
磁场
磁场现象的发现更早。在战国时期,我国就发明了指南针。与电场相仿,磁场是在一定空间区域内连续分布的向量场,描述磁场的基本物理量是磁感应强度矢量B,也可以用磁感线形象地表示。西莫恩·泊松发展出一种物理模型,比较能够描述磁场。泊松认为磁性是由磁荷产生的,同类磁荷相排斥,异类磁荷相吸引。他的模型完全类比现代静电模型;磁荷产生磁场,就如同电荷产生电场一般

然而,作为一个矢量场,磁场的性质(宏观)与电场颇为不同。
磁场是无源有旋的矢量场,磁力线是闭合的曲线簇,不中断,不交叉。从N出发,指向S
磁场的运动相对性是指与场源同速运动的观察者及其检测仪器都不能测到运动中的场源所产生的磁场,而与场源不同速时则可测到场源的磁场。例如在地球表面参考系中,我们测定静止于地球表面的电子不产生磁场,但是这个静止于地球表面的电子却在不停地随同地表进行自转并围绕太阳公转。又例如,使导线对外产生磁场的电流是大量电子定向运动的结果。该载流导线在对外产生磁场的同时,其中的每一个运动电子并不被与其同行的其它电子的磁场所干扰,因为所有同行的电子都具有同等磁化而无法感受到其它电子磁场的存在
磁极不能单独存在,无论把磁铁切多么小,都会出现新的磁极

磁场分为静磁场和动磁场。地球的磁场属于静磁场,电磁铁的磁场属于动磁场。
磁场性质
- 磁感应强度:与磁力线方向垂直的单位面积上所通过的磁力线数目,叫磁通密度,用B表示,单位为特斯拉(T)。
- 磁通量:磁通量是通过某一截面积的磁力线总数,用Φ表示,单位为韦伯(Weber),符号是Wb。 通过一线圈的磁通的表达式为:Φ=B·S(其中B为磁感应强度,S为该线圈的面积。) 1Wb=1T·m2
- 磁场强度:单位正电磁荷在磁场中所受的力被称为磁场强度(符号为H A/m),类比电荷。
安培分子流假说认为并不存在磁荷,自此磁场的强度多用磁感应强度(符号为B)表示。 但是在磁介质的磁化问题中,磁场强度作为一个导出的辅助量仍然发挥着重要作用。介质中,$H := \frac{B}{\mu_0} - M$ - 安培力:匀强磁场对通电直导线的作用力,即安培力与磁感应强度、电流和导线长度成正比。(左手定则)F=BILsinθ 矢量表达式:F=I×BL。
- 洛伦兹力:磁场会对电荷施加力。运动电荷在磁场中所受到的力以荷兰物理学家洛伦兹(H. A. Lorentz, 1853—1928)的姓氏命名,称为洛伦兹力(Lorentz force)。 (左手定则)F=qvBsinθ。矢量表达式:F=qv×B
与电场的关系
在很长一段时间里,人们把磁现象和电现象看成两种彼此独立的自然现象。直到1820年丹麦物理学家奥斯特(H.C.Oersted,1777-1851)发现了电流的磁效应之后,人们才逐渐认识到电和磁之间的内在联系。
经典物理学发现,变化的磁场产生电场,变化的电场产生磁场。这些实际是假设,这个假设基于电磁感应现象。 后来,麦克斯韦将各种电、磁方程整合,发展出麦克斯韦方程组,这方程组能够解释经典电学和磁学的各种现象。他提出了“分子涡流模型”,并成功地将安培定律加以延伸,增加入了一个有关于位移电流的项目,称为“麦克斯韦修正项目”。可以描述电磁波的行为,推导出电磁波方程。他又计算出电磁波的传播速度,发现这数值与光速非常接近。警觉的麦克斯韦立刻断定光波就是一种电磁波。后来,于1887年,海因里希·鲁道夫·赫兹做实验证明了这事实。麦克斯韦统一了电学、磁学、光学理论。
爱因斯坦在发展出狭义相对论的思想实验里,表明电场和磁场是处于不同参考系的观察者所观察到的同样现象。电场和磁场是电磁场的两面。设定两个参考系A和B,相对于参考系A,参考系B以有限速度移动。从参考系A观察为静止电荷产生的纯电场,在参考系B观察则成为移动中的电荷所产生的电场和磁场。
变化的电场产生磁场,那么磁铁是怎么形成的呢?磁铁上有电流吗?
磁铁对外没有电流,但是内部有电流,这就是安培分子流假说:在原子、分子等物质微粒内部,存在着一种环形电流——分子电流,分子电流使每个物质微粒都成为微小的磁体,它的两侧相当于两个磁极。一根铁棒,未被磁化的时候,内部各分子电流的取向是杂乱无章的,它们的磁场互相抵消,对外界不显磁性。当铁棒受到外界磁场的作用时,各分子电流的取向变得大致相同,铁棒被磁化,两端对外界显示出较强的磁作用,形成磁极。

现代物理学否定了原先流行的磁荷观。不过英国物理学家保罗·迪拉克在1931年利用数学公式预言了磁单极粒子的存在。当时他认为既然带有基本电荷的电子在宇宙中存在,那么理应带有基本“磁荷”的粒子存在。科学家仍没有放弃寻找磁单极粒子。如果找到了,电磁理论将要作重大修改。
磁铁能否永久保持其强度?磁铁一直对外做功,磁性会减弱甚至消失吗?
只要使磁铁远离对其磁性产生负面影响的因素(例如电源线、其他磁铁、高温等),理论上它将永久保持其磁性。
比如强磁质的特殊性质在高温下会失效,使得强磁质性质失效的临界温度叫做居里点。 这被解释为高温使得分子运动剧烈,磁铁内部的分子电流方向变得杂乱无章,磁场互相抵消,磁性消失。 当使用磁铁吸附物体或推开物体,是外部力量与磁场的能量相互转化,是能量从一种形式转化到另一种形式,只要磁铁内部排列不变,磁铁的磁性就不会减弱。
电磁波简介
机械波
在了解到电磁波前,自然界中还存在机械波。在机械波中,振动的传播需要具有弹性的介质。机械波分为横波和纵波。横波是振动方向垂直于波的传播方向,纵波是振动方向与波的传播方向一致。声波是一种纵波,水波是近似横波。地震波是一种复合波。描述波的物理量:波长λ、波速v、频率f
频率:波的频率就是波源的振动频率,也是所有质点的振动频率。是单位时间内完成周期振动的次数
波速:波在均匀介质中匀速传播的速率只与介质有关,而与频率无关。
波长:在波动中振动相位总是相同的两个相邻质点间的距离。对于横波,相邻的两个波峰或相邻的两个波谷之间的距离等于一个波长。
它们三者的关系是:v=λf
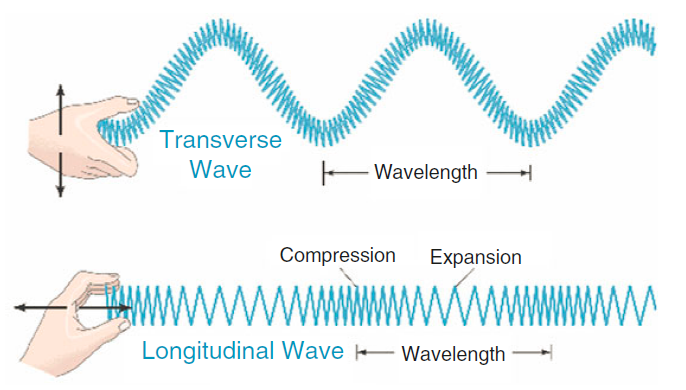
波具有干涉、衍射、偏振、折射、反射等现象。同时波还能传播能量。
电磁波
电磁波又叫电磁辐射,是指同相振荡且互相垂直的电场与磁场,是一种非机械波,在空间中以波的形式传递能量和动量,其传播方向垂直于电场与磁场的振荡方向是一种横波,和机械波一样,符合波理论。和机械波不同的是,它的传播不需要介质,在真空中也能传播。现代量子场论中光子被认为是电磁相互作用的媒介子。 光子静止质量为零。光子以光速运动,并具有能量、动量、质量。光具有波粒二象性

电磁波的波长和频率有关系:c=λf,其中c是光速,约等于3×10^8m/s。电磁辐射由低频率到高频率主要分为:无线电波、微波、红外线、可见光、紫外线、X射线和γ射线。人眼可接收到的电磁波,称为可见光(波长380~780nm)

在电动力学里,根据麦克斯韦方程组,随着时间变化的电场产生了磁场,反之亦然。因此,一个振荡中的电场会产生振荡的磁场,而一个振荡中的磁场又会产生振荡的电场,这样子,这些连续不断同相振荡的电场和磁场共同地形成了电磁波。电场,磁场都遵守叠加原理。因为电场和磁场都是矢量场,所有的电场矢量和磁场矢量都适合做矢量加运算。例如,一个行进电磁波,入射于一个介质,会引起介质内的电子振荡,因而使得它们自己也发射电磁波,因而造成折射或衍射等等现象。电碰波的能量一半存于电场,一半存于磁场。比如我们可以使用电场天线和磁场天线来“感知”电磁波中的电场和磁场
麦克斯韦方程组
麦克斯韦方程组有微分和积分表示,但等价。并且真空和介质略有不同,积分形式更容易理解一些,下边以真空中的麦克斯韦方程来了解。
- 高斯定律, 描述通过任意闭曲面的电通量与这闭曲面内的电荷之间的关系。
$$
\displaystyle \oiint _\mathbb{S} \mathbf {E} \cdot \mathrm {d} \mathbf {s} ={\frac {Q}{\varepsilon _{0}}}
$$
- Q: 闭曲面内的总电荷
- $\epsilon_0$是真空介电常数
- E: 电场强度
可见电通量只与电荷有关,电场是有源场
- 高斯磁场定律, 描述通过任意闭曲面的磁通量等于零。
$$
\displaystyle \oiint _\mathbb{S} \mathbf {B} \cdot \mathrm {d} \mathbf {s} =0
$$
- B: 磁感应强度
表明通过任意闭曲面的磁通量等于零,磁场是无源场,不存在单极子
- 法拉第电磁感应定律:时变磁场产生感应电场。
$$
\displaystyle \oint _{\mathbb{L}} \mathbf {E} \cdot \mathrm {d} \mathbf {l} =-{\frac {\mathrm {d} }{\mathrm {d} t}}\iint _\mathbb{S} \mathbf {B} \cdot \mathrm {d} \mathbf {s} =-{\frac {\mathrm {d} \Phi _{\mathbf {B} }}{\mathrm{d} t}}
$$
表明电动势(V)是磁通量的变化引起
- 麦克斯韦-安培定律:磁场可以通过以下两种方法产生:一种是靠传导电流(原本的安培定律),另一种是靠时变电场,称位移电流(麦克斯韦修正项)
$$
{\displaystyle \oint _{\mathbb {L} }\ \mathbf {B} \cdot \mathrm {d} {\boldsymbol {\ell }=\mu _{0}I+\mu _{0}\varepsilon _{0}{\frac {\mathrm{d} }{\mathrm {d} t}} \iint _\mathbb{S} \mathbf E \cdot \mathrm {d}s }=\mu _{0}I+\mu _{0}\varepsilon _{0}{\frac {\mathrm{d} \Phi _{\mathbf {E} }}{\mathrm {d} t}}}
$$
- $\mu_0$是真空磁导率
表明磁场环量由电流和电场的变化引起
电磁波的传播
通过一系列数学推导,可以得到真空中的波动方程:
$$
\begin{aligned}
% laplacian operator
\nabla ^{2} \mathbf {E} -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {E} }{\partial t^{2}}} &=0\
\nabla ^{2} \mathbf {B} -{\frac {1}{c^{2}}}{\frac {\partial ^{2}\mathbf {B} }{\partial t^{2}}} &=0
\end{aligned}
$$
称为双曲型偏微分方程, 其中
- $c=\frac{1}{\sqrt{\mu_0\epsilon_0}}$是真空中的光速
- $\nabla^2$是拉普拉斯算子,在直角坐标系中是:
$$
\nabla ^{2} =\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)
$$
波动方程描述了波在时空中传播的规律。对平面波,它的一个解是:
$$
\begin{align}
E = E_0 \cos(\omega t - kr + \phi) \
H = H_0 \cos(\omega t - kr + \phi)
\end{align}
$$
是和位置和时间有关的函数。
对比经典力学中的机械波方程一致:
$$
\nabla ^{2} \psi -{\frac {1}{v^{2}}}{\frac {\partial ^{2}\psi }{\partial t^{2}}} =0
$$
其中,$\psi$是波函数,v是波速
麦克斯韦方程组的局限
因为麦克斯韦方程组完全不能表达光子的概念,任何涉及到单独光子的现象,例如光电效应、普朗克定律、单光子探测器、电磁场的量子纠缠等等,假若使用麦克斯韦方程组来解释,都会遇到困难。对于这些案例,必须用量子电动力学的理论来给予解释
FDTD(时域有限差分法)
在实际中,电磁波的传播是一个非常复杂的问题,需要考虑介质、边界和干涉问题,不能简单用平面简谐波计算,需要用数值方法来求解,FDTD是一种数值求解电磁波传播的方法,它是一种时域方法,通过离散化空间和时间,将麦克斯韦方程组转化为差分方程,然后通过迭代求解。
转换差分需要后两个方程就可以了,因为前两个方程是关于电场和磁场的分布,而后两个方程是关于电场和磁场的变化,是关于时间的。
中心差分是一种常用的差分方法,它是用前后两个点的值的平均值来估计中间点的值。对于一维情况,中心差分的公式是:
$$
\frac{\partial f}{\partial x} \approx \frac{f(x+\Delta x) - f(x-\Delta x)}{2\Delta x}
$$
对时间和空间使用中心差分,可以得到麦克斯韦方程组的差分形式,简单起见,使用真空一维情况理解

可见,其中的每一项都可由它的前两项推导而来。
E 是在全时间步上、全空间,B 是在半时间步,半空间上计算(为何这样设计?而不是反过来)。如下:
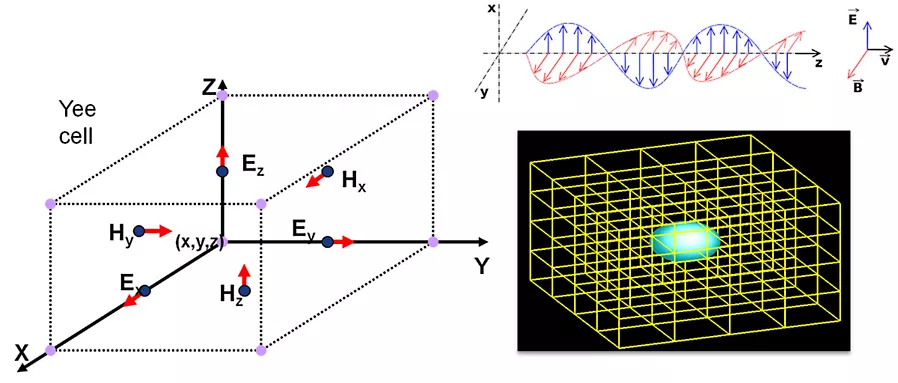
上述最简单的一维情况综合起来:
$$
\frac {\partial E_x}{\partial y} = \frac{\partial B_z}{\partial t}
$$
在空间和时间上求解:
令
$$y = j \Delta y, t = n \Delta t$$
离散化空间和时间,可以得到:

整理可以得到磁场和电场的更新方程:
$$
B_z(j+\frac{1}{2}, n+\frac{1}{2}) = B_z(j+\frac{1}{2}, n-\frac{1}{2}) + \frac{\Delta t}{\Delta y} (E_x(j+1, n) - E_x(j, n))
$$
$$
E_x(j, n+1) = E_x(j, n) + \frac{\Delta t}{\Delta y} (B_z(j+\frac{1}{2}, n+\frac{1}{2}) - B_z(j-\frac{1}{2}, n+\frac{1}{2}))
$$
可以写出 FDTD 的算法步骤:
initial field E, B by ??
for n = 0, nmax
for j = 0, jmax-1
update B
end
for j = 0, jmax
update E
end
end
FDTD(Finite-Difference Time-Domain)