从数学的角度判断车头距障碍的距离

在驾驶的过程中，我们总需要判断车头距离障碍物的距离，以确保安全驾驶。经常看到有文章从参照点的方式来估计距离。本文将从数学的角度，探讨如何通过简单的计算和测量，来估算车头与障碍物之间的距离。

基本原理

在使用参照点法时，我们通常会选择车头的阻档视线的某个位置为参照点，如果坐姿高，一般是车头引擎盖的前端位置，如果坐姿低，是前档风玻璃的下端位置。然后通过观察障碍物与参照点之间的相对位置，来判断距离。

数学模型

假设我们眼睛E到地面的高度为$H_e$，车头参照点R到地面的高度为$H_r$，E点到R点的水平距离为$D_{er}$，R在墙面上视线方向投影点O的高度为$H_o$，通过三角形的相似原理，我们就可以计算出车头R到障碍物O的水平距离$D_{ro}$。

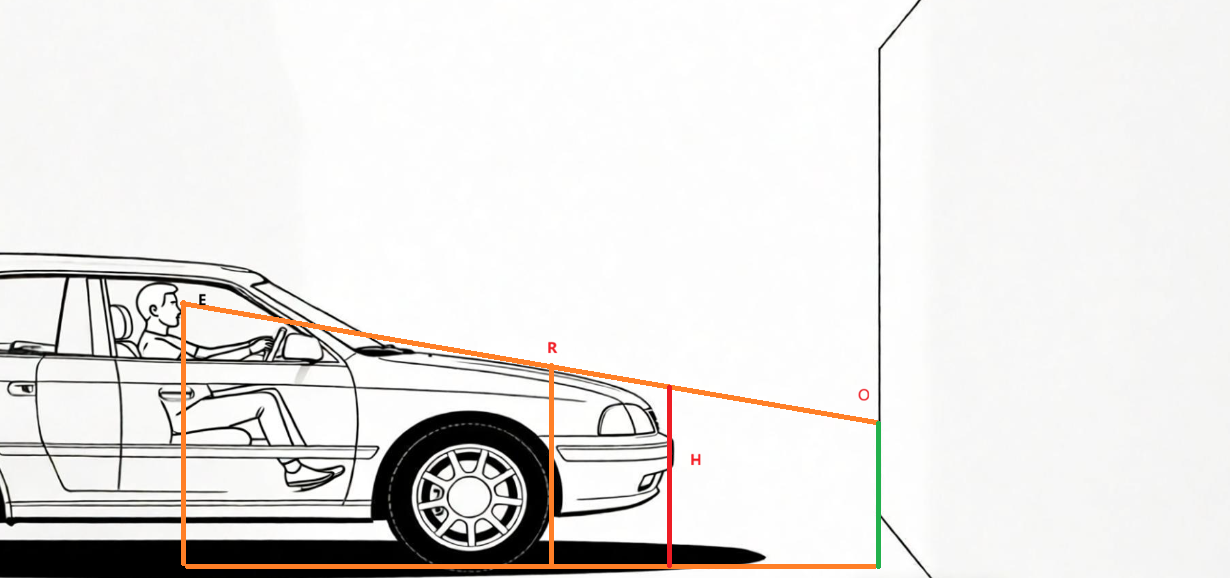
上图可以转化成下图的模型：

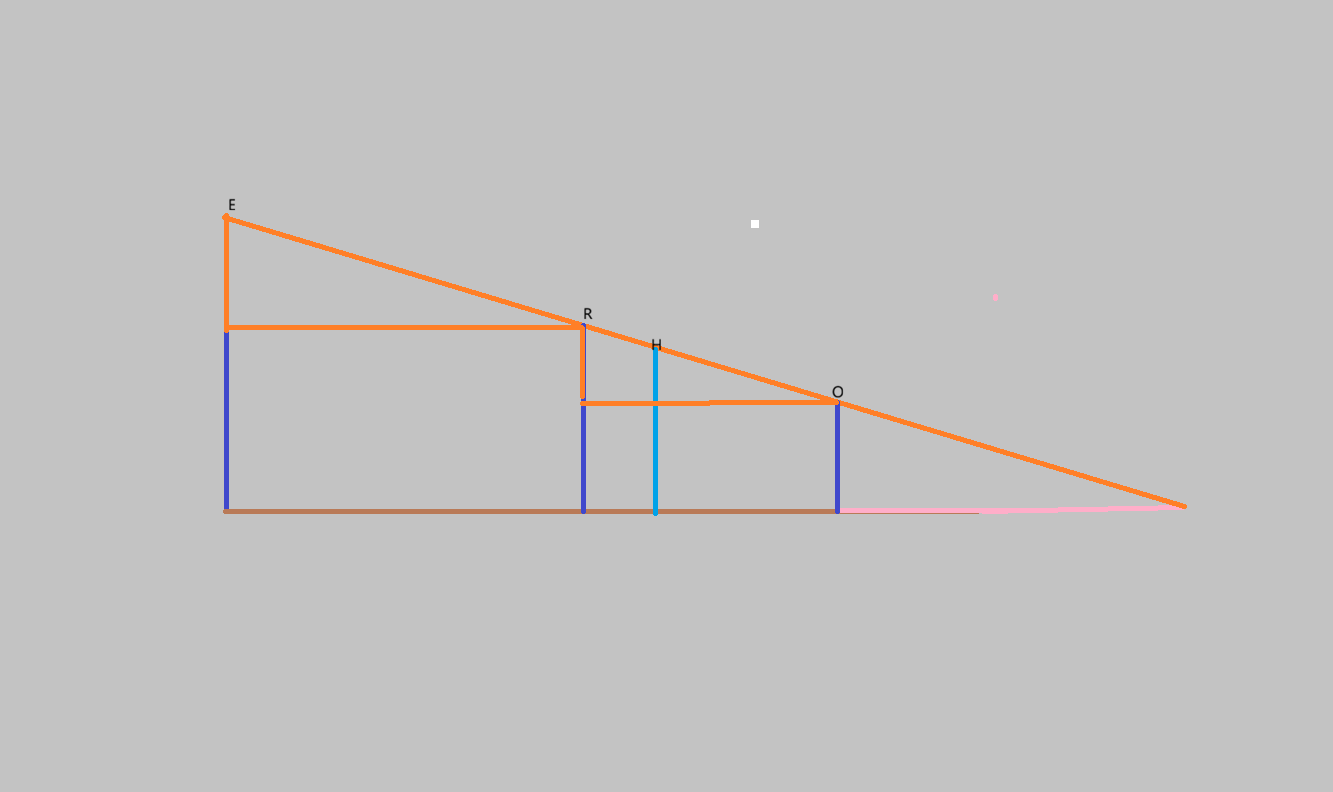
根据图中两个橙色相似三角形的性质，可以得到以下关系：
$$\frac{H_e - H_r}{D_{er}} = \frac{H_r - H_o}{D_{ro}}$$
通过变形，我们可以得到车头R到障碍物O的距离$D_{ro}$:
$$D_{ro} = D_{er} \cdot \frac{H_r - H_o}{H_e - H_r}$$

假设我们有以下已知量：

• 眼睛E到地面的高度$H_e$ = 1.5m
• 车头参照点R到地面的高度$H_r$ = 1m
• 我们坐位眼睛到参考点的水平距离为$D_{er}$ = 2.5m

那么，当我们观察在视线方向上与障碍物的交点O的高度$H_o$时，我们可以计算出车头R到障碍物O的距离$D_{ro}$。

• $H_o$ = 0m时，$D_{ro}$ = 2.5 * 1 / 0.5 = 5m，如文中所说，当眼睛刚好看到前车轮胎时，距离5m
• 当$H_o$ = 0.5m时，$D_{ro}$ = 2.5 * 0.5 / 0.5 = 2.5m
• 当$H_o$ = 0.7m时，$D_{ro}$ = 2.5 * 0.3 / 0.5 = 1.5m
• 当$H_o$ = 0.8m时，$D_{ro}$ = 2.5 * 0.2 / 0.5 = 1m
• 当$H_o$ = 0.9m时，$D_{ro}$ = 2.5 * 0.1 / 0.5 = 0.5m

但是这个距离是参考点距离墙面的距离，一般参考点都不是在车的最前方的车头位置，如果要计算车头前端到墙面的距离，还需要减去参考点R到车头前端的距离。这也是一个固定值$D_{rh}$。

$$D_{ro} = D_{er} \cdot \frac{H_r - H_o}{H_e - H_r} - D_{rh}$$

这也为什么能解释，轿车坐姿低时，参考点在前档风玻璃下端位置，当我看到轮胎下缘时，感觉实际距离比5m更近。

实际应用

在实际驾驶中，我们可以通过以下步骤来估算车头与障碍物的距离：

1. 测量高度：测量眼睛E到地面的高度$H_e$，车头参照点R到地面的高度$H_r$，眼睛E到参考点R的水平距离$D_{er}$，以及参考点R到车头前端的距离$D_{rh}$。
2. 观察障碍物：当驾驶时，观察障碍物O在视线方向上的投影点P的高度$H_o$。
3. 计算距离：因为公式中，$\frac {D_{er}}{H_e - H_r}$是一个常量K，我们可以预先计算好这个值，然后通过观察$H_o$，快速计算出车头到障碍物的距离$D_{ro}$。比如上面我的例子中，这个值是5。